Backpropagation (역전파)

인공 신경망을 학습시키기 위한 알고리즘 중 하나 신경망을 학습시키는 목표 중 하나는 도출된 예측값과 실제값의 차이 (오차)를 줄이기 위함이다 그렇기에 예측값과 실제값의 차이를 역전파를 통해 모든 가중치에 전달하여 갱신을 하며 궁극적으로 오차를 줄이는 기법이다

1. 노드가 가지고 있는 가중치 (weight)나 편향 (bias)같은 변수들을 어떻게 갱신 (update)하나?

2. 노드의 변수들을 어떻게 개별적으로 얼만큼 업데이트 하나?

Chain rule (연쇄법칙)을 이용해 위 두 가지 질문들을 해결할 수 있다

Chain rule (연쇄법칙)

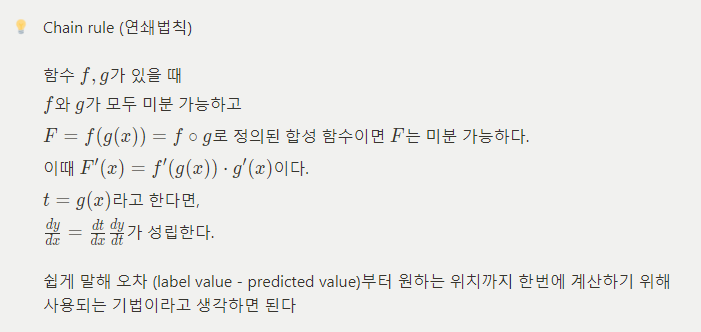
미분이 가능하다 = 기울기를 구한다 = 변화량을 구한다

즉 x가 변화했을 때 함수 g의 변화량, 함수 f의 변화량, 그리고 최종 값 F의 기여하는 함수 f와 g의 기여도를 찾는 것

Forward-propagation (순전파)

예측값을 도출하기 위해 변수와 가중치를 연산하는 것

데이터와 가중치를 연산하여 예측값을 도출하는 방법이라고 이해하면 된다

1. 연결된 데이터 $x$와 가중치 $w$를 연산 후 더한 값이 $z$

2. $z$를 활성화 함수 $a$로 연산

3. $a$와 $w$를 연산 후 더한 값이 $z$

4. $z$를 활성화 함수 $a$로 연산

   1. 최종층이면 연산 후 나온 값이 최종 예측값

      1. 그리고 실제값 $y$와 최종 예측값을 뺀 값이 오차다

   2. 아니라면 step 3과 4를 반복

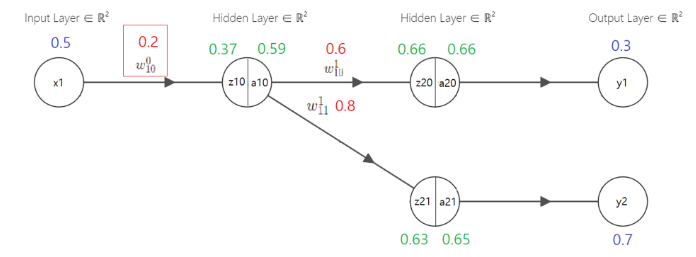
순전파 예시

$x, w, y$는 임의의 수를 정해 적어주었다

$z$와 $a$는 계산한 값을 표한다

직관적으로 표현하기 위해 activation function ($a$)는 sigmoid함수, cost function ($L$)은 mean squared error (MSE)함수를 사용했다

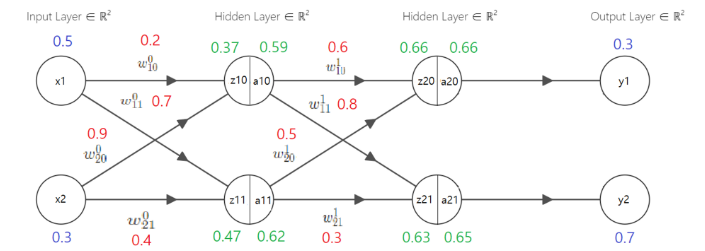
위 예시는 forward-propagation (순전파)을 한 예시를 보여준다

첫번째 hidden layer의 연산 법은 아래와 같다

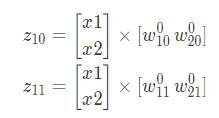
이를 풀어서 작성하면 아래와 같다

구한 z_{10}과 z_{11}의 값들을 activation function인 sigmoid를 사용해 a_{10}과 a_{11}을 구해주며 sigmoid 수식을 다음과 같다

이렇게 연산을 해서 구한 값들이 위 예제 그림에 보이는 값들이다

2번째 hidden layer 역전파 예시

순전파로 값들을 다 도출했으니 이제 역전파로 오차에 대한 변화량을 찾을 차례이다

먼저 cost function은 MSE를 사용하기로 결정했으며 수식을 아래와 같다

$y_i$는 정답, $\hat y_i$는 인공 신경망이 도출해낸 예측값이다

MSE와 가중치 업데이트 수식을 이용해 가중치의 변화량을 찾을 수 있다

가중치 업데이트 수식은 다음과 같다

\eta 는 한번에 얼마나 학습할지를 표현하고 {\partial L\over \partial w}는 어느 방향으로 학습할지를 표현한다

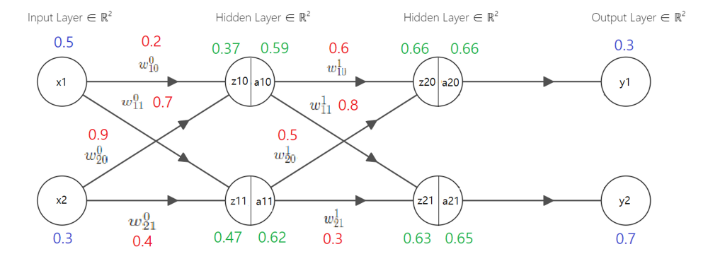
위 예제 그림 중 역전파를 이용해 w^1_{10}을 계산해 보자

Chain rule을 이용한다면 수식은 아래와 같다

먼저 \partial L \over \partial a_{20}를 풀어보자. L의 수식은 다음과 같다

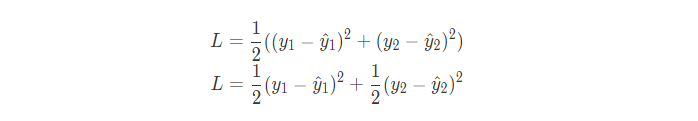
여기서 \hat y_1과 \hat y_2는 a_{20}과 a_{21}을 뜻하며 w^1_{10}만 업데이트 해보려고 하기에 편미분을 통해 a_{21}은 상수 취급하여 무시하고 합성함수의 편미분을 이용해 풀면 된다

계산결과인 0.36이 뜻하는 바는 $a_{20}$이 오차인 $L$에 0.36만큼 기여했다는 것을 의미한다

그럼 ${\partial a_{20} \over \partial z_{20}}$을 계산해보자. 먼저 알아야 할건 sigmoid의 미분이다

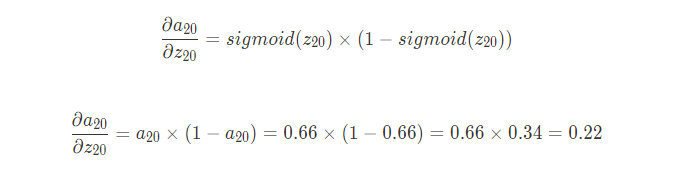
다음은 {\partial z_{20} \over \partial w^1_{10}}을 계산해보자. 위와 마찬가지로 편미분을 사용하기에 도출되는 값은 a_{10}이 된다

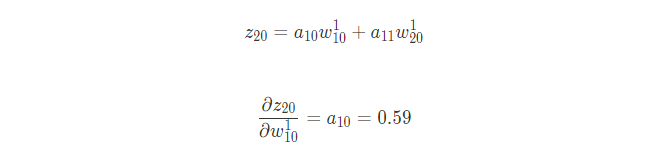
그럼 처음에 구하려고 했던 {\partial L\over \partial w^1_{10}}의 값은 다음과 같다

w^1_{10}이 기여한 값은 0.05가 되고 가중치 업데이트 수식을 이용해 가중치를 갱신할 수 있다

학습률은 사람이 정해줄 수 있는 하이퍼파라미터이며 일반적으로 0.1이하를 정하기에 임의로 0.1로 정했다

이렇게 해서 가중치 $w^1_{10}$은 0.6에서 0.595라는 값을 얻게 되었고 다른 가중치들도 위와 같은 과정을 거쳐 업데이트가 가능하다

1번째 hidden layer 역전파 예시

그럼 1번째 은닉층 계산에 사용되는 가중치 w^0_{10}을 업데이트 해보자

오차 L에 기여한 정도는 아래와 같이 나타낼 수 있다

그럼 {\partial L_1 \over \partial a_{10}}부터 구해보자

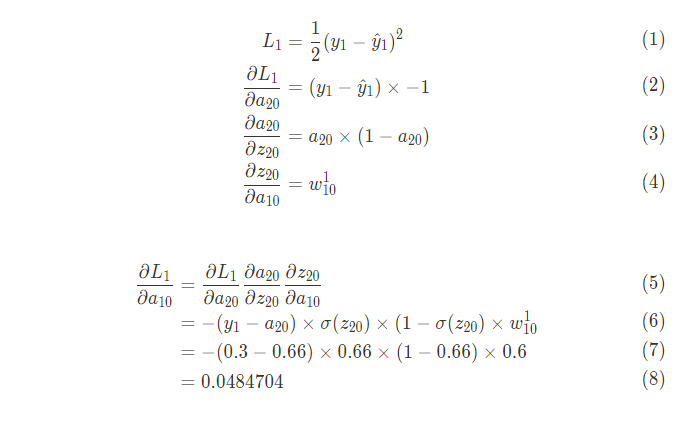
다음 {\partial L_2 \over \partial a_{10}}을 구해보자

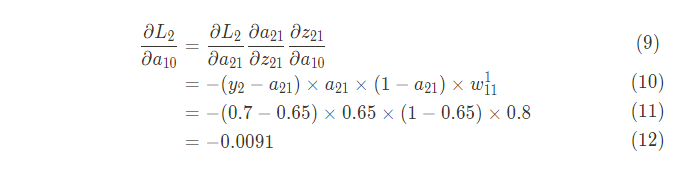
그럼 이제 {\partial L \over \partial w^0_{10}}을 구해보자

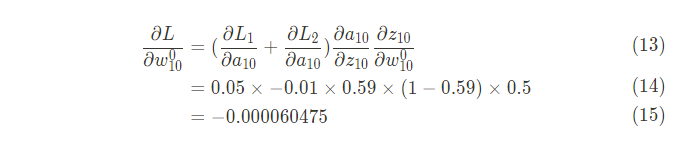
이를 토대로 가중치를 업데이트 해보자

그럼 가중치가 미미하게 변화하는 것을 볼수가 있다

이렇게 전체 가중치에 대해 backpropagation을 진행한 것을 1 epoch 진행했다고 하며 epoch이 진행될 수록 가중치가 갱신되며 오차가 줄어든다